上下文
设想你和朋友即将出国旅行。你会提前制定详细的行程安排,预订所有的酒店和餐厅吗?还是等到出发当天再试图购买机票?再想象一下,明天你和朋友准备在附近的城市漫步。你会事先制定一份精确的路线计划,还是等到出发前再决定乘坐哪种交通工具?
这两个情境体现了计划的细致程度与风险的平衡。在国际旅行中,我们通常倾向于制定详细计划,因为未知的因素和风险较高;而在城市漫步中,我们可能更愿意即兴决定,因为风险相对较低。类似地,在研发过程中,是否可以通过直接推进沙子级别的需求来快速前进?这与在黑暗中前行的抉择是相似的。这种不确定性状态,我们称之为潜在风险状态。
在软件开发中,估算的核心目的是帮助团队更好地管理风险、理解需求以及辅助设计。通过估算,团队能够对未来进行合理的预测,并制定有效的计划。然而,估算的另一个重要作用是校准团队成员对需求的理解,确保大家在同一基础上进行讨论和决策。因此,估算不仅是对工作量的预测,更是对项目各个关键方面的全面考量。
在研发过程中的估算,我们需要在以下两个关键点之间找到平衡:
风险控制
估算是控制风险的重要手段之一。当开发人员被问到估算时,他们通常会重新审视需求的复杂性和潜在风险。通过乒乓拆分 配合 轻斐估算,团队可以更准确地理解和评估需求的风险,从而避免因估算粒度过大而导致的潜在问题。
精简时间
我们花了无数的精力来尝试得到所谓更靠谱的估算,但最终无法摆脱其估算的本质。
然而,花费过多时间在估算上并不总是明智的。在我的经验中,无论是花费10天还是1天进行估算,项目的最终结果往往是相似的。然而,时间拖延可能导致团队在进入开发时对初期估算的信息遗忘。因此,快速 是敏捷估算的关键之一,需要在控制风险的同时,最大化地提高效率。
类似概念
Planning Poker (计划扑克)
计划扑克一般包含以下选择:
?, 0, ½, 1, 2, 3, 5, 8, 13, 20, 40, 100, ∞, 咖啡杯
使用流程如下:
- 准备牌组:每个团队成员拿到一套计划扑克牌,牌面上标有一系列数字(如斐波那契数列)和特殊符号(如“?”、“∞”)。
- 任务描述:产品负责人或项目经理简要描述要估算的任务或用户故事,确保所有成员都理解需求。
- 独立估算:每个团队成员根据对任务的理解,选择一张最能代表他们估算的扑克牌,且不与其他成员交流。
- 同时亮牌:所有成员同时展示他们选择的扑克牌,显示各自的估算结果。
- 讨论差异:如果大家的估算结果相差较大,团队进行讨论。通常会请选择最高和最低估算值的成员解释他们的理由。
- 重新估算:经过讨论后,团队成员再次进行独立估算并亮牌,直到达成共识或接近一致的估算结果。
- 记录结果:将最终的估算结果记录下来,用于规划和任务分配。
轻斐估算,与计划扑克不同的点是:
- 不需要大数字 ^no-need-big-numbers
- 13, 20, 40, 100, ∞:代表着风险,我们可能给出了一个数字其实有可能是因为这个数字比较大而已,遇到估算较大的需求就应该直接拆分,而不应该给出一个数值。
- 不需要0或½
- 这些需求可以简单的合并到一个新的需求条目之中,所以不应该存在。
- 不需要问号
- 我们太关注扑克的形式,就会拥有这样的卡片。问题不是重要的,尝试解决问题的待办推进更为重要。
- 不需要咖啡
- 需要咖啡侧面表现出估算的时间过长了,如果是一个快速过程不需要中间的休息过程。
- 不强制所有人员详细讨论所有需求
- 在团队中很多人是跟着走的,看似听懂的给出扑克牌其实没有意义。
- 关键点在于:当所有估算给出之后,团队每一个人是否认可这些估算。
Agile Estimating 2.0 (估算 2.0)
来自:Agile Estimating 2.0 – Cheat Sheet
- 初始排列:从已排序的故事卡片堆开始,将卡片按大小从左到右排列,最小的在左边,最大的在右边,相同或相似大小的卡片垂直分组。
- 第一张卡片放置:将第一张(排名最高的)故事卡片放在桌子或墙板的中央。
- 回合制估算:团队成员依次进行估算。每轮,玩家可以选择:
- 从堆顶拿一张新卡片并根据估算大小放置在适当位置。
- 调整已放置卡片的位置,重新估算其大小。
- 讨论规则:在玩家估算时,其他成员只能提出澄清性问题,不应表达个人意见。
- 最后调整:在所有卡片估算完毕后,每位成员可以再移动一次卡片,进行最后的调整。
- 分配故事点:根据卡片组分配故事点,使用伪斐波那契数列(1, 2, 3, 5, 8, 13, 20, 40, 100),或使用2的幂(1, 2, 4, 8, 16, 32, 64, 128)。
- 相对估算:数字代表每个故事的相对大小/工作量,例如,3个故事点约为2个故事点的1.5倍工作量,8个故事点是4个故事点的两倍工作量。
轻斐估算,与估算 2.0不同的点是:
- 只使用斐波那契数列的12358
- 其他数列需要更多的解释
- 不使用过大的数字
- 不强调相对估算
- 只使用12358几个数字,并且强调之前估算是1的需求,未来相似需求的估算也应该是1。(自然就是相对估算)
- 团队可以选出若干动手给出估算的人,而不是全员动手
- 不给出估算的人可以提出问题,比如测试人员或刚刚加入团队的人。
关键特征
概念
轻斐数列(12358)
估算过程只使用12358中的一个数字,通过这样的方式来粒度平准化 需求。粒度小于1的需求需要合并若干需求给出一个估算。估算给出8的需求建议进行拆分。
- 业务角度可以提出反馈
- 虽然估算是技术角度的事情,但复杂度的确认需要可以从业务角度进行反馈。比如质疑为什么之前某个需求是1,但是这个需求是2。
- 不同工种协同的不同任务,可以合并在一个需求之中成为几个任务。比如测试的工作、前端、后端等。
- 估算描述需求复杂度
- 操作几个数据库表?有多少界面?有多少交互能力?有没有动画效果?算法复杂?几个第三方接口?这些都可以作为衡量需求复杂度的一个维度。可以给出一个简单的对照表进行估算。
- 不计入估算
- 等待时间
- 等待第三方的完成,等待某些角色提供文档,等待上线调试等不应该算入估算。
- 缺陷
- 缺陷是期望功能的失效,新特性是之前没有期望的功能缺失。可以明确到底是缺陷还是新特性。
- 技术任务
- 技术任务无法被业务角度感知到,所以需要渐进式进行技术优化,而不是等待遗留成巨量的技术债务。
- 等待时间
然而,需要注意的是,估算本质上是一种对未来的预测。如果在项目管理中赋予估算过多的使命,可能会导致行为关注点的偏移。比如,团队可能会更关注如何达到预定的估算数字,而忽视了实际任务的质量和成果。这种偏移不仅降低了工作的创造性,也可能导致项目最终偏离初衷。因此,在使用估算时,必须保持对其目的的清晰理解,避免其成为过度控制的工具。
潜在风险状态(Potential Risk)
“潜在风险状态”不仅仅是研发中的一种常见现象,它实际上是项目管理中必须时刻警惕和管理的关键领域。识别这些潜在风险,理解其来源,并采取适当的措施来缓解或消除这些风险,是确保项目顺利进行的基础。
1. 缺乏估算
任何没有进行估算的需求或任务,都是充满潜在风险的。这类需求往往属于沙子级别的需求,因其不确定性高,容易导致项目的不确定性增加。因此,没有估算的需求通常意味着更高的风险。
2. 假设的风险
在研发中,假设是我们对未来情况的预测或前提条件。在估算过程中,假设的存在与否都会带来潜在风险:
- 没有假设的估算:如果在没有明确假设的情况下进行估算,往往基于不完整的信息或过于乐观的预测。这种情况容易忽略潜在的未知变量或意外情况,导致项目进度或成本的严重偏差。换句话说,没有假设的估算实际上是风险中的风险。
- 有假设的估算:即使在有假设的情况下,估算也可能存在潜在风险。假设本质上是对未来的一种预测,但这些预测未必与实际情况吻合。如果假设不成立,估算结果可能会严重偏离预期,从而影响项目的准确性和可控性。
3. 估算为8
在估算中,数字8代表数列中的最大值,通常用于描述最复杂、最不确定的需求。给出8的估算值,可能意味着团队无法进一步细化需求的复杂性,这时候,需求的风险和不确定性往往超出预期。因此,任何被评估为8的需求都应被视为需要进一步探讨的高风险需求。
角色
推动者可以兼职挑战者的角色,但执行者是独立的。
推动者(Prompter)
推动者可能是需求或业务相关人员,也可以是引导者。
职责:
- 明确估算范围:明确哪些需求是这次估算的范围,哪些可以不进行估算。
- 关注时间的高效性:
- 询问估算执行者为什么不能估算,给假设是否可以估算。
- 询问估算执行者,估算成8的需求是否可以拆分,是否可以给出假设。
- 记录一切需要讨论的问题,形成某个人有期限的待办。
- 记录一切大家达成一致的信息。
估算执行者(Executor)
估算执行者一般是资深开发人员,或非常了解技术细节的架构师。
职责:
- 确定估算数字。
- 明确假设内容。
- 说出不能估算的原因,明确如何做才能得到估算。
挑战者(Challenger)
挑战者一般由测试人员、资历浅的人员、团队管理者组成。
职责:
- 对执行者提出进一步的问题
- 之前相似的需求是某个估算,但这个为什么是这个估算?
- 某某情况考虑了吗?
- 明确提出的问题得到恰当跟进
过程
下面是从估算执行者(Executor)角度的流程图:
flowchart TD
start1([开始])
end1([结束])
start1 --> 没估算
没估算 --> try[尝试<br>估算]
try -- 太大拆分 --> try
try -- 太小合并 --> try
try -- 明确假设 --> 假设
假设 --> try
try -- 沟通明确 --> try
try -- 回答问题 --> try
try -- 12358 --> 有估算
try -. 有阻碍 .-> 待办
有估算 -. 8 .-> 潜在风险
有估算 -. 没假设 .-> 潜在风险
假设 .-> 潜在风险
有估算 --> end1
待办 .-> end1
- 推动者明确估算和参与者范围,驱动估算执行者开始:
- 确定范围:推动者明确本次估算的需求范围,并决定挑战者的参与人数,确保合适的人参与估算。
- 驱动开始:推动者指示估算执行者开始估算,并确保相关信息和资源到位。
- 估算执行者提出假设并进行初步估算:
- 提出假设:根据需求复杂性,估算执行者提出假设。
- 初步估算:使用轻斐数列对需求进行初步估算。
- 挑战者质疑估算并推动讨论:
- 质疑合理性:挑战者提出关键问题,验证估算合理性。
- 推动验证:促使团队进一步讨论和验证假设。
- 推动者记录问题,推动需求拆分或合并:
- 记录问题:推动者记录讨论中出现的问题。
- 推动调整:推动估算执行者拆分或合并需求,调整估算。
- 估算执行者调整估算,确保团队一致认可:
- 调整估算:根据反馈调整估算,确保团队一致认可。
- 确认结果:确保最终估算结果得到团队一致认可。
- 推动者记录待办事项并跟进:
- 记录跟进:推动者记录待办事项并分配责任,确保问题得到解决。
- 推动完成:推动整个估算流程顺利完成,并总结改进。
相关概念
估算的关键点
估算过程中有两个关键点,可以帮助我们快速得到相对准确的结果。这两个关键点是:
1. 样本数量大
任何估算都可能存在偏差,但从统计学角度来看,如果样本数量足够大,整体的估算结果将趋于平衡个体的偏差。如图所示:
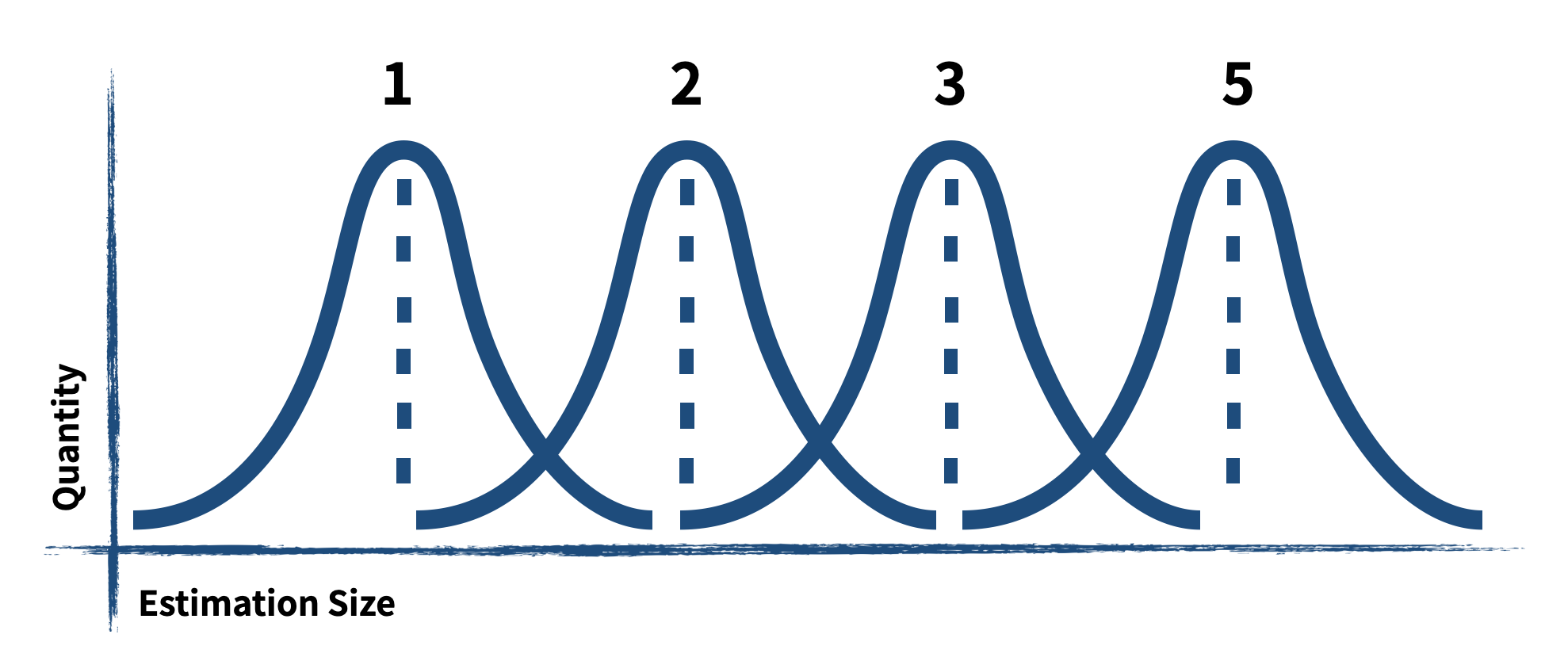
重要的是,如果你在进行估算时,将当前需求与之前估算完成的需求进行相对比较,那么这就符合了统计学上的“样本数量大”这一要求。但如果每次只关注眼前的少量需求进行估算,你将面临更大的不确定性。
2. 个体粒度小
如果允许使用100作为估算的最大单位,最终可能会出现一些需求被估算为100,但这个估算值是否准确反映了需求的实际大小呢?往往不是。实际上,这种估算值可能意味着需求的复杂性远超100,甚至可能达到1000或10000,只是我们在更大数字上缺乏具体的划分依据。
相比之下,较小粒度的需求估算更为可靠。小粒度需求的变化范围较小,且在拆分过程中,变化的部分可以被隔离和分解。切分方法可以参考 乒乓拆分。
在进入实际开发阶段之前,建议团队再次对需求进行估算。这次估算的重点不在于获得精确的数字,而是通过重新审视需求来更清楚地了解实现思路,并进一步管理潜在的风险。尽管这次估算不用于统计分析,但它能有效帮助团队确认他们的设计和实现路径是否合理,从而提高开发的成功率。
为什么估算扑克不建议使用
- 打扑克太占用时间;
- 太多用不到的扑克牌数字(除了1、2、3、5其他都用不到);
- 还需要带着的东西,也可能丢;
放弃估算
是否选择使用估算,实际上取决于具体的上下文和对风险的可控性,而不是某种理论上的正确与否。你可以选择使用估算,也可以选择不使用。这就像饮食一样,选择什么食物应当根据身体的实际需求来决定。然而,如果你无法准确感知身体的需要,各种营养专家的建议就显得尤为重要。
尤其是在知识工作领域,估算的挑战更为显著。知识工作的创造性和不确定性,使得简单的估算方法难以反映工作的复杂性和价值。在这样的背景下,强行使用估算可能会导致对知识工作的低估,并抹杀创新的可能性。因此,在进行估算时,必须结合具体的工作性质,合理调整估算方法和预期。
我们不能断言这些专家的建议是错误的,你可以尝试他们的方法,观察身体的反应,然后进行调整。本文建议在大多数情况下使用估算,正如营养专家建议合理饮食一样。
如果你参与的是一个拥有无限预算和人力资源的自筹资金项目,那么或许无需依赖详细的估算,只需计算投入与产出的比例,找到平衡即可。然而,如果这是一个甲乙方合作的项目,且项目实施过程中充满了不确定性和风险,放弃使用估算可能会带来巨大的挑战和隐患。
几年前,“看板之父”戴维·安德森准备撰写一本关于看板实践的书籍,并派一位研究人员来到中国收集素材。这位研究人员来到中国后,发现看板上每一张卡片都标有明确的交付时间、估算以及进度跟踪信息。他感到非常惊讶,认为这些并不是看板方法的核心,甚至认为这更像是一种过度的压力和控制。
但事实上,这种做法反映了对现实的适应与承认。在面对高度耦合的系统、人员素质参差不齐以及版本发布的高压环境时,这种方法在中国得以广泛应用,实际上也是一种合理的应对策略。在类似的情况下,你可能也会采用与我们相似的方式来管理项目。
估算方法对比
在敏捷开发中,避免使用线性数列(如1、2、3、4、5……)进行估算是关键。线性数列容易给团队带来精确的错觉,似乎每个数字之间的差异都可以精确衡量,但实际上,它们无法充分表现出需求的不确定性和复杂性。这种错觉可能导致团队在面对复杂需求时低估风险,从而影响项目的进展。
斐波那契数列(12358)
使用1、2、3、5、8这些数字来估算需求的大小。这些数字简单明确,方便直接用于计算,也容易让团队达成一致。适合大多数团队,能帮助快速给出估算结果,并且业务人员也能轻松理解。
二的幂数列(Power of Two)(1248)
使用1、2、4、8等数字来估算。这些数字跨度更大,适合将复杂的需求快速拆分为较大的块。适合需要粗略估算的情况,但可能不如斐波那契数列细致。
衬衫大小法(T-Shirt Sizing)
用“XXS、XS、S、M、L、XL、XXL”这些尺寸标签来表示需求的大小。虽然直观,但最终还是需要转换为数字来计算。适合快速分类需求,但要注意后续转换为数字可能会增加复杂性。
这些方法的共同点在于避免了线性数列,通过非线性数列更有效地反映需求的复杂度和不确定性,从而帮助团队做出更合理的决策。
原子敏捷性的考虑
从原子敏捷性的角度来看,估算过程应着眼于快速适应和灵活应对需求变化,而不仅仅是追求数字的精确性。通过 更广阔的视角,团队在估算时不仅关注当前需求的具体细节,还要考虑潜在的风险和未来的变化,这使得估算更具战略意义。更强悍的纪律 强调在估算过程中保持严格的拆分和合并原则,以确保需求的粒度适当,并且在执行中不被琐碎的细节所拖累。同时,使用 更明确的灰度 的方法,团队能够在详细计划和即兴应对之间找到平衡,不会因过于追求完美的计划而失去敏捷的优势。这些原则共同指导团队在不确定性中保持敏捷,确保估算既能控制风险,又能促进项目的灵活推进。